Losses in source resistance can lower the efficiency by 10% or more, exclusive of loss in the DC-DC converter! If the converter has adequate input voltage, its output will be normal and there may be no obvious indication that power is being wasted. Fortunately, testing the input efficiency is a simple matter (see the Source section).

A large source resistance can cause other, less obvious effects. In extreme cases, the converter's input can become bistable, or its output can decrease under maximum load conditions. Bistability means that the converter exhibits two stable input conditions, each with its own efficiency. The converter output is normal, but system efficiency may be drastically affected (see How to Avoid Bistability).

Should this problem be solved simply by minimizing the source resistance? No, because the practical limits and cost/benefit trade-offs posed by the system may suggest other solutions. A prudent selection of power-supply input voltage, for example, can considerably minimize the need for low source resistance. Higher input voltage for a DC-DC converter limits the input current requirement, which in turn lessens the need for a low source resistance. From a systems standpoint, the conversion of 5V to 2.5V may be far more efficient than the conversion of 3.3V to 2.5V. Each option must be evaluated. The goal of this article is to provide analytic and intuitive tools for simplifying the evaluation task.

A systems view
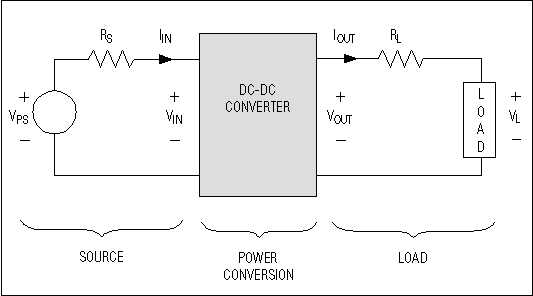
As shown in Figure 1, any regulated power-distribution system can be divided into three basic sections: source, regulator(s) (a DC-DC converter in this case), and load(s). The source can be a battery or a DC power supply that is either regulated or unregulated. Unfortunately, the source also includes all the dissipative elements between the DC voltage and load: voltage-source output impedance; wiring resistance; and the resistance of contacts, PC-board lands, series filters, series switches, hot-swap circuits, etc. These elements can seriously degrade system efficiency.

Figure 1. A regulated power-distribution system has three basic sections.

Calculation and measurement of the source efficiency is very simple. EFF_SOURCE equals (power delivered to the regulator) / (power provided by VPS) multiplied by 100%:

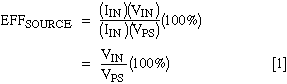
Assuming that the regulator draws a negligible amount of current when unloaded, you can measure source efficiency as the ratio of V_IN with the regulator at full load to V_IN with the regulator unloaded.

The regulator (DC-DC converter) consists of a controller IC and associated discrete components. Its characterization is described in the manufacturer's data sheet. Efficiency for the DC-DC converter (EFF_DCDC) equals (power delivered by the converter) / (power delivered to the converter) multiplied by 100%:

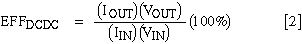
As specified by the manufacturer, this efficiency is a function of input voltage, output voltage, and output load current. It's not unusual for the efficiency to vary no more than a few percent over a load current range exceeding two orders of magnitude. Because the output voltage is fixed, we can say the efficiency varies only a few percent over an "output-power range" exceeding two orders of magnitude.

DC-DC converters are most efficient when the input voltage is closest to the output voltage. If the input variation is not extreme with respect to the data sheet specifications, however, the converter's efficiency can usually be approximated as a constant between 75% and 95%:

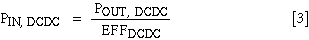
This discussion treats the DC-DC converter as a two-port black box. For those interested in the nuances of DC-DC converter design, see References 1-3.

The load includes the device to be driven and all dissipative elements in series with it, such as PC-trace resistance, contact resistance, cable resistance, etc. Because the DC-DC converter's output resistance is included in the manufacturer's data sheet, that quantity is specifically excluded. Load efficiency (EFF_LOAD) equals (power delivered to the load) / (power delivered by the DC-DC converter) multiplied by 100%:

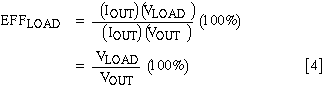
The key to optimum system designs is in analyzing and understanding the interaction between the DC-DC converter and its source. To do this we first define an ideal converter, then calculate the source efficiency, then test our assumptions against measured data from a representative DC-DC converter-in this case, the MAX1626 buck regulator.

The ideal DC-DC converter
An ideal DC-DC converter would have 100% efficiency, operate over arbitrary input- and output-voltage ranges, and supply arbitrary currents to the load. It would also be arbitrarily small and available for free! For this analysis, however, we assume only that the converter's efficiency is constant, such that input power is proportional to output power:

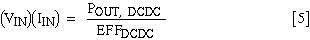
For a given load, this condition implies that the input current-voltage (I-V) curve is hyperbolic and exhibits a negative differential-resistance characteristic over its full range (Figure 2). This plot presents I-V curves for the DC-DC converter as a function of increasing input power. For real systems with dynamic loads, these curves are also dynamic. That is, the power curve moves farther from the origin as the load demands more current.

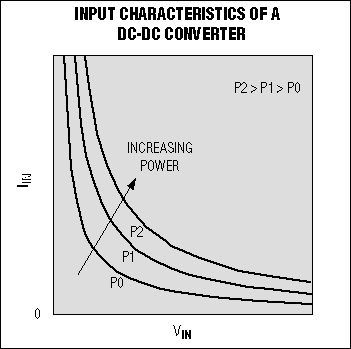
Figure 2. These hyperbolas represent constant-power input characteristics for a DC-DC converter.

Considering a regulator from the input port instead of the output port is an unusual point of view. After all, regulators are designed to provide a constant-voltage (sometimes constant-current) output. Their specifications predominantly describe the output characteristics (output-voltage range, output-current range, output ripple, transient response, etc.). The input, however, displays a curious property: within its operating range it acts as a constant-power load (Reference 4). Constant-power loads are useful in the design of battery testers, among other tasks.

Calculating source efficiency
We now have enough information to calculate the source's power dissipation and therefore its efficiency. Because the open-circuit value of source voltage (V_PS) is given, we need only find the DC-DC converter's input voltage (V_IN). From equation [5], solving for I_IN:

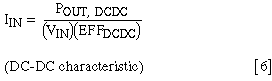
I_IN can also be solved in terms of V_PS, V_IN, and R_S:

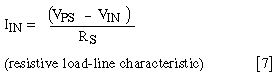
Equate the expressions from equations [6] and [7] and solve for V_IN:

To understand their implications, it is very instructive to visualize equations [6] and [7] graphically (Figure 3).

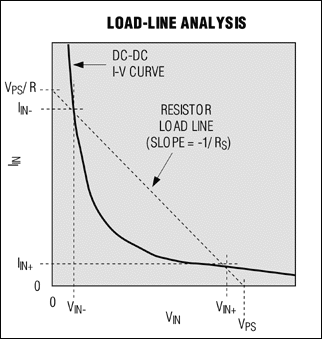
Figure 3. This plot superimposes a load line for source resistance on the DC-DC converter's I-V curve.

The resistor load line is a plot of all possible solutions of equation [7], and the DC-DC I-V curve is a plot of all possible solutions of equation [6]. The intersections of these curves, representing solutions to the pair of simultaneous equations, define stable voltages and currents at the DC-DC converter's input. Because the DC-DC curve represents constant input power, (V_IN+)(I_IN+) = (V_IN-)(I_IN-). (The + and - suffixes refer to the two solutions predicted by equation [8], and correspond to the ± signs in the numerator.)

The optimum operating point is at V_IN+ / I_IN+, which minimizes I_IN²R_S loss by drawing minimum current from the power supply. The other operating point causes large power dissipation in any dissipative components between V_PS and V_IN. System efficiency drops dramatically. But you can avoid such problems by keeping R_S low enough. The source efficiency [(V_IN / V_PS) · 100%] is simply equation [8] divided by V_PS:

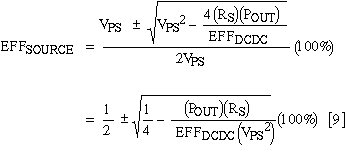
It's easy to get lost in the equations, and therein lies the value of the load-line analysis plot of Figure 3. Note, for example, that if the series resistance (R_S) equals zero, the resistor load-line slope becomes infinite. The load line would then be a vertical line passing through V_PS. At this point V_IN+ = V_PS and the efficiency would be 100%. As R_S increases from 0W, the load line continues to pass through V_PS but leans more and more to the left. Concurrently, V_IN+ and V_IN- converge on V_PS / 2, which is also the 50% efficiency point. When the load line is tangent to the I-V curve, equation [8] has only one solution. For larger R_S, the equation has no real solution and the DC-DC converter no longer functions properly.

DC-DC converters-theory vs. practice
How do these ideal-input curves compare with those of an actual DC-DC converter? To examine this question, a standard MAX1626 evaluation kit (Figure 4) was configured for an output voltage of 3.3V and a load resistor of 6.6W. We then measured the input's I-V curve (Figure 5). Several nonideal characteristics were evident immediately. Note, for example, that for very low input voltages the input current is zero. A built-in undervoltage lockout (denoted as V_L) ensures that the DC-DC converter is off for all input voltages below V_L. Otherwise, large input currents could be drawn from the power supply during start-up.

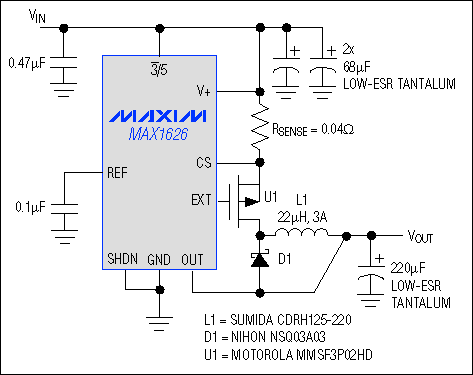
Figure 4. A standard DC-DC converter circuit illustrates the ideas of Figure 3.

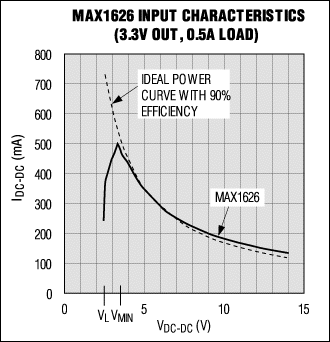
Figure 5. Above V_MIN, the MAX1626 input I-V characteristic closely matches that of a 90%-efficient ideal device.

When V_IN exceeds V_L, the input current climbs toward a maximum that occurs when V_OUT first reaches the preset output voltage (3.3V). The corresponding input voltage (V_MIN) is the minimum required by the DC-DC converter to produce the preset output voltage. For V_IN > V_MIN, the constant-power curve for 90% efficiency closely matches the MAX1626 input curve. Variations from the ideal are caused primarily by small variations in DC-DC converter efficiency as a function of its input voltage.

How to avoid bistability
The power-supply designer must also guarantee that the DC-DC converter never becomes bistable. Bistability is possible in systems for which the load line intersects the DC-DC converter curve at or below V_MIN / I_MAX (Figure 6).

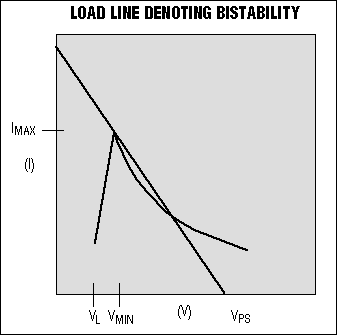
Figure 6. A closer look at the intersection points indicates a possibility of bistable and even tristable operation.

Depending on the load line's slope and position, a system can be bistable or even tristable. Note that a lower V_PS value can allow the load line to intersect at a single point between V_L and V_MIN, resulting in a system that is stable, but nonfunctional! As a rule, therefore, the load line must not touch the cusp of the DC-DC converter curve and must not move below it.

In Figure 6, the load-line resistance (R_S, which has a value of -1/slope) has an upper limit called R_BISTABLE:

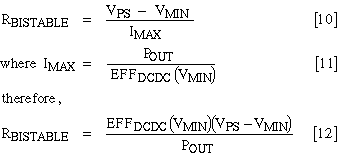
The source resistance (R_S) should always be smaller than R_BISTABLE. If this rule is broken, you risk highly inefficient operation or a complete shutdown of the DC-DC converter.

An actual case
It might be helpful to plot, for an actual system, the relationship shown in equation [9] between source efficiency and source resistance (Figure 7). Assume the following conditions:

V_PS = 10V   Open-circuit power-supply voltage
V_MIN = 2V   Minimum input voltage that ensures proper operation
P_IN = 50W   Power to the DC-DC converter's input (P_OUT / EFF_DCDC).

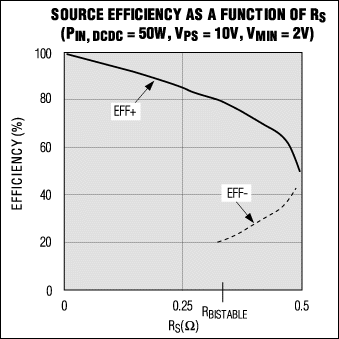
Figure 7. This plot of source efficiency vs. source resistance indicates multiple values of efficiency for a given R_S.

Using equation [12], R_BISTABLE can be calculated as 0.320W. Subsequently, a plot of equation [9] shows that source efficiency drops as R_S increases, losing 20% at R_S = R_BISTABLE. Note: this result cannot be generalized. You must perform the calculations for each application. One component of R_S is the finite output resistance found in all power supplies, determined by the load regulation and usually defined as:

A 5V / 10A power supply with 1% load regulation, for example, would have only 5.0mW of output resistance-not much for a 10A load.

Source efficiency for common applications
It's useful to know how much source resistance (R_S) can be tolerated and how this parameter affects system efficiency. R_S must be less than R_BISTABLE, as stated earlier, but how much lower should it be? To answer this question, solve equation [9] for R_S in terms of EFF_SOURCE, for EFF_SOURCE values of 95%, 90%, and 85%. R_S95 is the R_S value that yields a 95% source efficiency for the given input and output conditions. Consider the following four example applications using common DC-DC converter systems.

Example 1 derives 3.3V from 5V with a load current of 2A. For 95% source efficiency, be careful to keep the resistance between the 5V source and the DC-DC converter's input well under 162mW. Notice that R_S90 = R_BISTABLE, by coincidence. This value of R_S90 also implies that the efficiency could as easily be 10% as 90%! Note that system efficiency (as opposed to source efficiency) is the product of source efficiency, DC-DC converter efficiency, and load efficiency.

 Example 1. Application Using a MAX797 or MAX1653 DC-DC Converter (I_OUT = 2A)

Example 2 is similar to Example 1 except for output-current capability (20A vs. 2A). Notice that the series-resistance requirement for 95% source efficiency is 10 times lower (16mW vs. 162mW). To achieve this low resistance, use 2oz. copper PC traces.

 Example 2. Application Using a MAX797 or MAX1653 DC-DC Converter (I_OUT = 20A)

Example 3 derives 1.6V at 5A from a source voltage of 4.5V (i.e., 5V-10%). The system requirement of 111mW for R_S95 can be met, but not easily.

 Example 3. Application Using a MAX1710 DC-DC Converter with Separate +5V Supply (V_PS = 4.5V)

Example 4 is the same as Example 3, but with higher supply voltage (V_PS = 15V instead of 4.5V). Notice the useful trade-off: a substantial increase in the difference between input and output voltages has caused an efficiency drop for the DC-DC converter alone, but the overall system efficiency is improved. R_S is no longer an issue because the large R_S95 value (>1W) is easily met. A system with an input filter and long input lines, for example, can maintain a source efficiency of 95% or more without special attention to line widths and connector resistances.

 Example 4. Application Using a MAX1710 DC-DC Converter with Separate +5V Supply (V_PS = 15V)

Conclusion
When looking at DC-DC converter specifications, it is tempting to maximize efficiency by setting the supply voltage as close to the output voltage as possible. This strategy, however, can increase costs by placing unnecessary limitations on elements such as the wiring, connectors, and trace layout. System efficiency may even suffer. The analytic tools presented in this article should make such power-system trade-offs more intuitive and obvious.

References
(1) Erickson, Robert W. Fundamentals of Power Electronics.Chapman and Hall, 1997.

(2) Lenk, Ron. Practical Design of Power Supplies. IEEE Press & McGraw Hill, 1998.

(3) Gottlieb, Irving M. Power Supplies, Switching Regulators, Inverters and Converters. Second Edition, TAB Books, 1994.

(4) Wettroth, John. "Controller Provides Constant Power Load." EDN, March 14, 1997.